- Mi 26 April 2017
- MetaAnalysis
- Peter Schuhmacher
- #Python, #Statistics
Einfache lineare Regression
Einfache Methoden für Datenfluss und Statistik mit Python, Pandas, NumPy, StatsModels, Seaborn, Matplotlib
Das Beispiel stammt aus:
Reinhold Hatzinger, Kurt Hornik, Herbert Nagel (2011): R - Einführung durch angewandte Statistik, Pearson Studium, 465pp, ISBN978-3-8632-6599-1 , siehe auch hier
Dort könnten auch unter Extras/CWS die Input-Daten gefunden werden. Das nachfolgende Beispiel ist aus Kapitel 9.2 (Mehrere metrische Variablen), die verwendete Datendatei: gewicht.csv.
Im Beispiel liegen Daten zum Körpergewicht vor, das einerseits erfragt und anderseits mittels Waage gemessen wurde.
import numpy as np
import pandas as pd
import statsmodels.api as sm
import statsmodels.formula.api as smf
import seaborn as sns
import matplotlib.pyplot as plt
sns.set(style="ticks")
%matplotlib inline
Daten
angabe;waage
83;88,0
64;70,1
94;94,2
73;76,8
79;81,1
Die Daten liegen in einer CSV-Datei vor. Oben sind nur die ersten paar Zeilen davon angezeigt. Sie können mit pd.read_csv direkt in ein Pandas DataFrame eingelesen werden. Dabei muss mitgeteilt werden, dass ";" als Trennzeichen auftritt. In der zweiten Spalte müssen die "," durch "." ersetzt werden. Da die zweite Spalte danach als string vorliegt, wird sie mit pd.to_numeric in einen numerischen Wert umgewandelt.
f10Dir = r"C:/gcg/7_Wissen_T/eBücher/R-HatzingerHornikNagel/R-Begleitmaterial/Daten\\"
f10Name= r"gewicht.csv"
f10 = f10Dir+f10Name
dg = pd.read_csv(open(f10, newline=''), sep=';') # set ; as delimiter and import the data as pd.DataFrame
dg['waage'] = dg['waage'].str.replace(",",".") # replace the coma by a point
dg['waage'] = pd.to_numeric(dg['waage']) # transform the string into numerical value
dg.head(4) # display the first few lines of the DataFrame
| angabe | waage | |
|---|---|---|
| 0 | 83 | 88.0 |
| 1 | 64 | 70.1 |
| 2 | 94 | 94.2 |
| 3 | 73 | 76.8 |
Darstellung der Daten
Mit Seaborn können die Daten dargestellt werden. Die Regressionsgerade sowie die Häufigkeitsverteilungen werden automatisch berechnet und geplottet.
sns.jointplot(x="waage", y="angabe", data= dg, kind="reg");
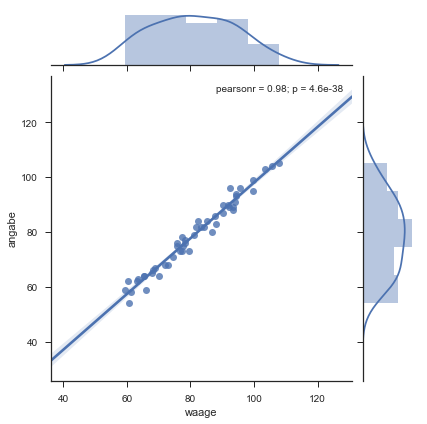
Parameter der Regressionsgerade
Wir berechnen nun die Regression mit StatsModels. Die gewünschte Regressionsbeziehung kann mit formula='angabe ~ waage ' in einem Format angegeben werden, wie es bei R üblich ist: y=angabe soll durch x=waage ausgedrückt werden. Die Ergebnisparameter liegen als pd.DataSeries vor, also ein 1-dimensionales DataFrame.
estimation = smf.ols(formula='angabe ~ waage ', data=dg).fit()
p = estimation.params
print(type(p))
print(p)
<class 'pandas.core.series.Series'>
Intercept -3.522249
waage 1.015543
dtype: float64
Verwendung der Regressionsgerade
Mit den Regressionsparametern drücken wir die Regressionsgerade aus. Für die x-Werte bilden wir einen NumPy-array, und die y-Werte berechnen wir mit der Geradengleichung. Mit Matplotlib plotten wir die Daten und die Gerade.
x = np.linspace(0,120,2)
y = p[0] + p[1]*x
fig,ax = plt.subplots()
ax.plot(x,y,'-')
ax.plot(dg['waage'],dg['angabe'],'o')
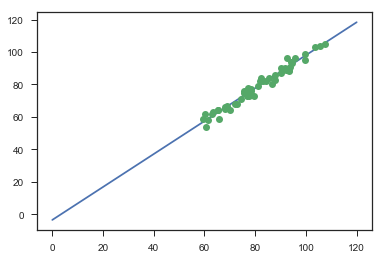
Von den StatsModels-Ergebnissen drucken wir die vollständige Zusammenfassung aus.
estimation.summary()
| Dep. Variable: | angabe | R-squared: | 0.970 |
|---|---|---|---|
| Model: | OLS | Adj. R-squared: | 0.969 |
| Method: | Least Squares | F-statistic: | 1529. |
| Date: | Tue, 12 Sep 2017 | Prob (F-statistic): | 4.62e-38 |
| Time: | 16:14:35 | Log-Likelihood: | -112.78 |
| No. Observations: | 50 | AIC: | 229.6 |
| Df Residuals: | 48 | BIC: | 233.4 |
| Df Model: | 1 | ||
| Covariance Type: | nonrobust |
| coef | std err | t | P>|t| | [0.025 | 0.975] | |
|---|---|---|---|---|---|---|
| Intercept | -3.5222 | 2.132 | -1.652 | 0.105 | -7.808 | 0.764 |
| waage | 1.0155 | 0.026 | 39.107 | 0.000 | 0.963 | 1.068 |
| Omnibus: | 0.153 | Durbin-Watson: | 1.858 |
|---|---|---|---|
| Prob(Omnibus): | 0.926 | Jarque-Bera (JB): | 0.318 |
| Skew: | -0.105 | Prob(JB): | 0.853 |
| Kurtosis: | 2.671 | Cond. No. | 525. |
Lineare Regression mit scipy
slope, intercept, r_value, p_value, std_err = st.linregress(dg['waage'], dg['angabe'])
print('scipy lingress: ',slope, intercept)
scipy lingress: 1.01554288925 -3.52224854645
Lineare Regression mit numpy
f_poly = np.polyfit(dg['waage'], dg['angabe'], 1)
print('numpy polyfit : ', f_poly)
numpy polyfit : [ 1.01554289 -3.52224855]
Function fitting with scipy
from scipy.optimize import curve_fit
def func(x, a, b): return a * x + b
popt, pcov = curve_fit(func, dg['waage'], dg['angabe'])
print(popt)
[ 1.01554289 -3.52224855]
```python
``````
