- Mi 26 April 2017
- MetaAnalysis
- Peter Schuhmacher
- #Python, #Statistics
Das Beispiel stammt aus:
Reinhold Hatzinger, Kurt Hornik, Herbert Nagel (2011): R - Einführung durch angewandte Statistik, Pearson Studium, 465pp, ISBN978-3-8632-6599-1 , siehe auch hier
Dort könnten auch unter Extras/CWS die Input-Daten gefunden werden. Das nachfolgende Beispiel ist aus Kapitel 9.4 (Mehrere metrische Variablen), die verwendete Datendatei: gebrauchtwagen.csv.
Im Beispiel liegen Daten zu Preis, Meilen, Servicehäufigkeit, Garagenparkierung und Farbe von Fahrzeugen vor. Es soll ein Prädiktor für die Preisbildung erstellt werden.
import numpy as np
import pandas as pd
import statsmodels.api as sm
import statsmodels.formula.api as smf
import seaborn as sns
import matplotlib.pyplot as plt
sns.set(style="ticks")
%matplotlib inline
Daten
Preis;Meilen;Service;Garage;Farbe
5318;37388;2;0;1
5061;44758;2;0;1
5008;45833;2;0;3
5795;30862;4;1;3
5784;31705;4;1;2
5359;34010;2;0;2
5235;45854;3;1;1
Die Daten liegen in einer CSV-Datei vor. Oben sind nur die ersten paar Zeilen davon angezeigt. Sie können mit pd.read_csv direkt in ein Pandas DataFrame eingelesen werden. Dabei muss der Lese-Funktion mitgeteilt werden, dass ";" als Trennzeichen auftritt. Alle Daten liegen nun als integer-Werte vor, auch die kategorialen Daten wie zur Farbe oder zur Garagierung.
f10Dir = "C:\gcg\\7_Wissen_T\eBücher\R-HatzingerHornikNagel\R-Begleitmaterial\Daten\\"
f10Name= "gebrauchtwagen.csv"
dg = pd.read_csv(open(f10Dir+f10Name,
newline=''),delimiter=';') # set ; as delimiter and import the data as pd.DataFrame
dg.head(7) # display the first few lines of the DataFrame
| Preis | Meilen | Service | Garage | Farbe | |
|---|---|---|---|---|---|
| 0 | 5318 | 37388 | 2 | 0 | 1 |
| 1 | 5061 | 44758 | 2 | 0 | 1 |
| 2 | 5008 | 45833 | 2 | 0 | 3 |
| 3 | 5795 | 30862 | 4 | 1 | 3 |
| 4 | 5784 | 31705 | 4 | 1 | 2 |
| 5 | 5359 | 34010 | 2 | 0 | 2 |
| 6 | 5235 | 45854 | 3 | 1 | 1 |
Darstellung der Daten
Mit Seaborn können die Daten dargestellt werden. Die Regressionsgerade sowie die Häufigkeitsverteilungen werden automatisch berechnet und geplottet.
sns.lmplot(x="Meilen", y="Preis", row="Garage", col="Farbe", data=dg,
ci=None, palette="muted", size=4,
scatter_kws={"s": 50, "alpha": 1});
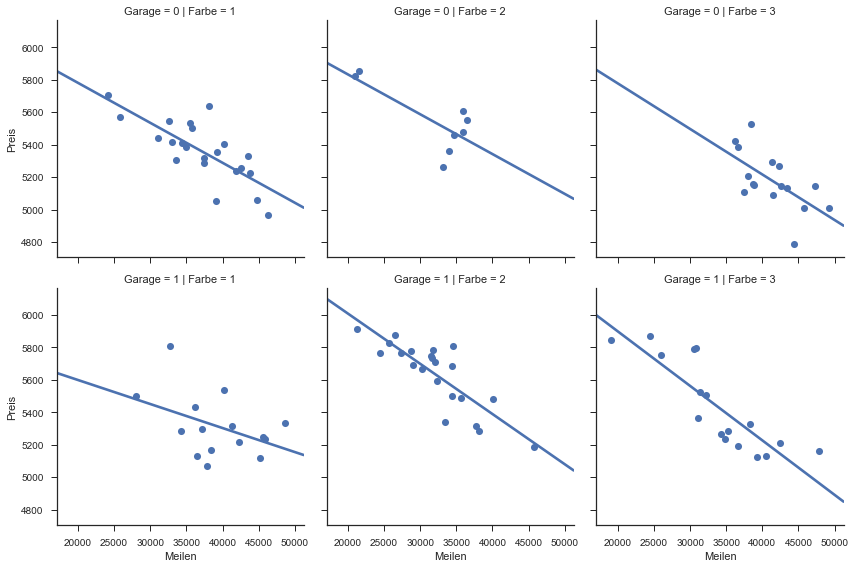
Analyse mit den metrischen Daten
Wir berechnen nun die Regression mit StatsModels, vorerst mit den metrischen Daten. Die gewünschte Regressionsbeziehung kann mit
in einem Format angegeben werden, wie es bei R üblich ist: y=Preis soll durch x1=Meilen und x2=Service ausgedrückt werden.
Wenn die formula-Methode zur Eingabe des Regressionsmodelles verwendet wird, so wird ein allfälliges intercept (\(p_0\)) von StatsModels automatisch beigefügt. Im Eingabeformat mit Numpy-Arrays müsste der Benutzer das intercept (\(p_0\)) explizit einfügen oder weglassen.
Die Ergebnisparameter liegen als pd.DataSeries vor, also ein 1-dimensionales DataFrame.
estimP1 = smf.ols(formula='Preis ~ Meilen + Service ', data=dg).fit()
p = estimP1.params # hier sind die Parameter enthalten
print(p)
estimP1.summary() # Asudruck der vollständigen Zusammenfassung
Intercept 6206.128356
Meilen -0.031463
Service 135.837493
dtype: float64
| Dep. Variable: | Preis | R-squared: | 0.974 |
|---|---|---|---|
| Model: | OLS | Adj. R-squared: | 0.974 |
| Method: | Least Squares | F-statistic: | 1822. |
| Date: | Tue, 12 Sep 2017 | Prob (F-statistic): | 1.19e-77 |
| Time: | 16:55:26 | Log-Likelihood: | -512.89 |
| No. Observations: | 100 | AIC: | 1032. |
| Df Residuals: | 97 | BIC: | 1040. |
| Df Model: | 2 | ||
| Covariance Type: | nonrobust |
| coef | std err | t | P>|t| | [0.025 | 0.975] | |
|---|---|---|---|---|---|---|
| Intercept | 6206.1284 | 24.966 | 248.581 | 0.000 | 6156.577 | 6255.679 |
| Meilen | -0.0315 | 0.001 | -49.788 | 0.000 | -0.033 | -0.030 |
| Service | 135.8375 | 3.903 | 34.807 | 0.000 | 128.092 | 143.583 |
| Omnibus: | 3.778 | Durbin-Watson: | 2.280 |
|---|---|---|---|
| Prob(Omnibus): | 0.151 | Jarque-Bera (JB): | 2.103 |
| Skew: | -0.039 | Prob(JB): | 0.349 |
| Kurtosis: | 2.294 | Cond. No. | 2.21e+05 |
Weiterverwendung der Ergebnisse
Mit den Regressionsparametern drücken wir die Regressionsebene aus. Dies ist mit 3-dimensionaler Grafik möglich, solang nur 2 Eingangsgrössen x1 und x2 vorliegen. Für die x1- und x2-Werte bilden wir je einen NumPy-array, welche wir zu einem meshgrid erweitern. Damit können wir die y-Werte der Regressionsebene berechnen. Mit Matplotlib plotten wir die Daten und die Ebene.
Mmin = min(dg["Meilen"]); Mmax = max(dg["Meilen"]);
Smin = min(dg["Service"]); Smax = max(dg["Service"]);
Pmin = min(dg["Preis"]); Pmax = max(dg["Preis"]);
print("Meilen : min, max = ", Mmin,",", Mmax )
print("Service: min, max = ", Smin,",", Smax)
print("Preis : min, max = ", Pmin,",", Pmax)
x1 = np.linspace(Mmin, Mmax, 6) # 1-dim array für x1 = Meilen
x2 = np.linspace(Smin, Smax, 6) # 1-dim array für x2 = Service
x1,x2 = np.meshgrid(x1, x2) # 2-dim array für x1 und x2
y = p[0]*np.ones_like(x1) + p[1]*x1 + p[2]*x2 # Ebenen-Gleichung
Meilen : min, max = 19057 , 49223
Service: min, max = 0 , 5
Preis : min, max = 4787 , 5911
from mpl_toolkits.mplot3d import Axes3D # 3-dim Grafik erstellen
from matplotlib import cm
from matplotlib.ticker import LinearLocator, FormatStrFormatter
import matplotlib.pyplot as plt
fig = plt.figure()
ax = fig.gca(projection='3d')
surf = ax.plot_surface(x1, x2, y, rstride=1, cstride=1, cmap=cm.coolwarm,
linewidth=0, antialiased=True) # Regressionsebene
ax.scatter(dg["Meilen"], dg["Service"], dg["Preis"]+440) # Daten
ax.set_zlim(2000, 6400)
ax.zaxis.set_major_locator(LinearLocator(10))
ax.zaxis.set_major_formatter(FormatStrFormatter('%.02f'))
fig.colorbar(surf, shrink=0.5, aspect=5)
plt.show()
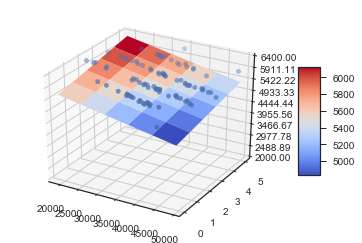
Analyse mit den kategorialen Daten
Wir schliessen nun auch die kategorialen Daten wie die Farbe (Werte: 1, 2, 3) oder die Garagierung der Fahrzeuge (0 = nein, 1 = ja) in die Analyse ein. Würden die Farben als Begriffe wie "blau", "rot" oder "schwarz" vorliegen, dann wäre StatsModels in der Lage, diese automatisch als kategoriale Daten zu erkennen und zu behandeln. Da sie aber als integer-Werte vorliegen, müssen wir StatsModels explizit mitteilen, dass sie nicht metrisch sondern kategorial behandelt werden sollen. Dies erfolgt recht einfach, indem die Werte mit C() ins Regressionsmodel eingegeben werden. In R spricht man dann auch davon, "die Daten als Faktor beifügen"
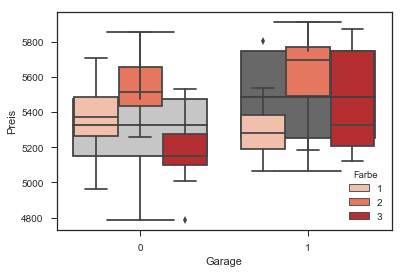
Ein Blick auf die Daten in Boxplot-Form zeigt, dass garagierte Fahrzeuge höhere Preise erzielen (vgl. graue Boxen), und es macht den Eindruck, dass innerhalb der Farben die Farbe Nr. 2 höhere Preise zu erzielen vermag als die andern(vgl.rote Boxen).
sns.boxplot(x="Garage", y="Preis", data=dg, palette="Greys");
sns.boxplot(x="Garage", y="Preis", hue="Farbe", data=dg, palette="Reds" );
Wir berechnen zuerst ein Modell für
und dann für
Die Ergebnistabellen zeigen anhand der t- und p-Werte, dass die Koeffizienten für die Farbe nicht signifikant sind, d.h. die Farben unterscheiden sich in ihrer Wirkung auf den Preis nicht signifikant voneinander.
estimP2 = smf.ols(formula='Preis ~ Meilen + Service + C(Garage)', data=dg).fit()
q = estimP2.params # hier sind die Parameter enthalten
print(type(q))
print(q)
#estimP2.summary() # Asudruck der vollständigen Zusammenfassung
<class 'pandas.core.series.Series'>
Intercept 6187.365916
C(Garage)[T.1] 19.007410
Meilen -0.031137
Service 134.541218
dtype: float64
estimP3 = smf.ols(formula='Preis ~ Meilen + Service + C(Garage)+ C(Farbe)', data=dg).fit()
r = estimP3.params # hier sind die Parameter enthalten
print(type(r))
print(r)
estimP3.summary() # Asudruck der vollständigen Zusammenfassung
<class 'pandas.core.series.Series'>
Intercept 6197.324575
C(Garage)[T.1] 20.454997
C(Farbe)[T.2] -10.438274
C(Farbe)[T.3] -6.703134
Meilen -0.031331
Service 135.185787
dtype: float64
| Dep. Variable: | Preis | R-squared: | 0.976 |
|---|---|---|---|
| Model: | OLS | Adj. R-squared: | 0.974 |
| Method: | Least Squares | F-statistic: | 751.9 |
| Date: | Tue, 12 Sep 2017 | Prob (F-statistic): | 3.88e-74 |
| Time: | 16:33:32 | Log-Likelihood: | -509.83 |
| No. Observations: | 100 | AIC: | 1032. |
| Df Residuals: | 94 | BIC: | 1047. |
| Df Model: | 5 | ||
| Covariance Type: | nonrobust |
| coef | std err | t | P>|t| | [0.025 | 0.975] | |
|---|---|---|---|---|---|---|
| Intercept | 6197.3246 | 28.027 | 221.119 | 0.000 | 6141.676 | 6252.973 |
| C(Garage)[T.1] | 20.4550 | 8.639 | 2.368 | 0.020 | 3.303 | 37.607 |
| C(Farbe)[T.2] | -10.4383 | 11.498 | -0.908 | 0.366 | -33.267 | 12.391 |
| C(Farbe)[T.3] | -6.7031 | 9.924 | -0.675 | 0.501 | -26.408 | 13.002 |
| Meilen | -0.0313 | 0.001 | -44.874 | 0.000 | -0.033 | -0.030 |
| Service | 135.1858 | 4.197 | 32.210 | 0.000 | 126.852 | 143.519 |
| Omnibus: | 0.814 | Durbin-Watson: | 2.267 |
|---|---|---|---|
| Prob(Omnibus): | 0.666 | Jarque-Bera (JB): | 0.930 |
| Skew: | -0.157 | Prob(JB): | 0.628 |
| Kurtosis: | 2.647 | Cond. No. | 2.56e+05 |
ANOVA (Analysis of Variances)
In der Varianzanalyse werden mit einem F-Test die Anteile der Variablen auf das Gesamtergebnis bewertet. In diesem Beispiel ist nur die Farbe nicht signifikant.
table = sm.stats.anova_lm(estimP3, typ=2)
print(table)
sum_sq df F PR(>F)
C(Garage) 9.362784e+03 1.0 5.606652 1.994089e-02
C(Farbe) 1.581404e+03 2.0 0.473491 6.243016e-01
Meilen 3.362746e+06 1.0 2013.690498 2.766973e-65
Service 1.732516e+06 1.0 1037.470903 1.407394e-52
Residual 1.569745e+05 94.0 NaN NaN
Es können auch ganze Modelle miteinander verglichen werden. Das einfachere Model estimP2 erscheint in der Tabelle mit dem Index 0 auf der ersten Zeile. Seine Residualquadratsumme ist kaum grösser als diejenige des umfangreicheren Modelles estimP3. Es ist damit vertretbar, das einfachere Modell zu verwenden.
table = sm.stats.anova_lm(estimP2,estimP3, typ=1)
print(table)
df_resid ssr df_diff ss_diff F Pr(>F)
0 96.0 158555.953796 0.0 NaN NaN NaN
1 94.0 156974.549379 2.0 1581.404417 0.473491 0.624302
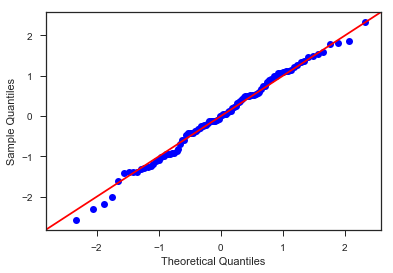
Normalverteilung der Residuen
Für die graphische Überprüfung, ob die Residuen normalverteilt sind, steht der QQ-Plot zur Verfügung. Mit den gesetzten Befehlsparameter werden die Parameter für die t-Verteilung mit bestimmt.
resP3 = estimP3.resid # residuals
fitP3 = estimP3.fittedvalues # fitted values
import scipy.stats as stats
fig = sm.qqplot(resP3, stats.t, fit=True, line='45')
plt.show()
Lillifors test for normality, Kolmogorov Smirnov test with estimated mean and variance
Der Kolmogorov Smirnov Test ist ein testtheoretisches Verfahren, das die Residuen auf Normalverteilung prüft.
kstest = sm.stats.diagnostic.kstest_normal(resP3, pvalmethod='approx')
print("Kolmogorov Smirnov Test :", kstest)
print("Residuen Mittelwert :", np.mean(estimP3.resid))
print("Residuen Standardabweichung :", np.std(estimP3.resid))
Kolmogorov Smirnov Test : (0.047867552271722208, 0.81426179797264298)
Residuen Mittelwert : 6.168340405565686e-08
Residuen Standardabweichung : 39.62001380346251
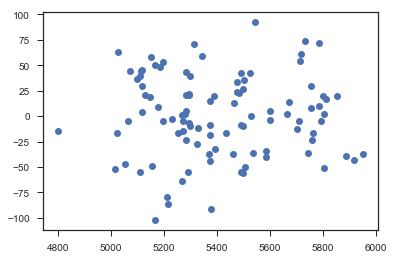
Plot: fitted Values vs Residuum
Im Residuen-Plot, mit den vorhergesagten Werten auf der x-Achse und den Residuen auf der y-Achse, sind keine Muster erkennbar. Die Voraussetzungen für die Regression wurden vermutlich erfüllt.
plt.plot(fitP3,resP3,'o')
plt.show()
Weitere Ergebnisse
estimP3 ist als der Output der ols-Funktion ein (programmiertechnisches) Objekt, dem ziemliche viele Attribute mitgegeben werden. Diese können abgerufen werden mit estimP3.attribut . Eine Liste der verfügbaren Attribute erhält man mit dem Befehl dir(estimP3)
dir(estimP3)
['HC0_se',
'HC1_se',
'HC2_se',
'HC3_se',
'_HCCM',
'__class__',
'__delattr__',
'__dict__',
'__dir__',
'__doc__',
'__eq__',
'__format__',
'__ge__',
'__getattribute__',
'__gt__',
'__hash__',
'__init__',
'__init_subclass__',
'__le__',
'__lt__',
'__module__',
'__ne__',
'__new__',
'__reduce__',
'__reduce_ex__',
'__repr__',
'__setattr__',
'__sizeof__',
'__str__',
'__subclasshook__',
'__weakref__',
'_cache',
'_data_attr',
'_get_robustcov_results',
'_is_nested',
'_wexog_singular_values',
'aic',
'bic',
'bse',
'centered_tss',
'compare_f_test',
'compare_lm_test',
'compare_lr_test',
'condition_number',
'conf_int',
'conf_int_el',
'cov_HC0',
'cov_HC1',
'cov_HC2',
'cov_HC3',
'cov_kwds',
'cov_params',
'cov_type',
'df_model',
'df_resid',
'diagn',
'eigenvals',
'el_test',
'ess',
'f_pvalue',
'f_test',
'fittedvalues',
'fvalue',
'get_influence',
'get_prediction',
'get_robustcov_results',
'initialize',
'k_constant',
'llf',
'load',
'model',
'mse_model',
'mse_resid',
'mse_total',
'nobs',
'normalized_cov_params',
'outlier_test',
'params',
'predict',
'pvalues',
'remove_data',
'resid',
'resid_pearson',
'rsquared',
'rsquared_adj',
'save',
'scale',
'ssr',
'summary',
'summary2',
't_test',
'tvalues',
'uncentered_tss',
'use_t',
'wald_test',
'wald_test_terms',
'wresid']
