.

.

.

.

.

HealthyNumerics

HealthyNumerics

HealthPoliticsEconomics | Quant Analytics | Numerics

Basic Stats 02: A mechanical approach to the Bayesian rule

Intro

The Bayesian rule

$$ P(A \mid B) = \frac{P(B \mid A) \cdot P(A)}{P(B)} $$

seems to be a rather abstract formula. But this impression can be corrected easely when considering a simple practical application. We call this approach mechanical because for this type of application there is no philosphical dispute between frequentist's and bayesian's mind set. We will just use in a mechanical/algorithmical manner the cells of a matrix. In this section we

  • formulate a prototype of a probability problem (with red and green balls that have letters A and B printed on)
  • summarize the problem in a basically 2x2 matrix (called contingency table)
  • use the frequencies first
  • replace them by probalities afterwards and recognize what conditional probablities are
  • recognize that applying the Bayesian formula is nothing else than walking from one side of the matrix to the other side
$$ $$

A prototype of a probability problem

Given:

  • 19 balls
  • 14 balls are red, 5 balls are green
  • among the 14 red balls, 4 have a A printed on, 10 have a B printed on
  • among the 5 green balls, 1 has a A printed on, 4 have a B printed on

Typical questions: - we take 1 ball. - What is the probabilitiy that it is green ? - What is the probabilitiy that it is B under the precondition it's green ?

We will use Pandas to represent the problem and the solutions

import matplotlib.pyplot as plt
from IPython.core.pylabtools import figsize
import numpy as np
import pandas as pd
pd.set_option('precision', 3)
$$ $$

Contingency table with the frequencies

The core of the representation is a 2x2 matrix that summarizes the situation of the balls with the colors and the letters on. This matrix is expanded with the margins that contain the sums. - sum L stands for the sum of the letters - sum C stands for the sum of the colors

columns = np.array(['A', 'B'])
index   = np.array(['red', 'green'])
data    = np.array([[4,10],[1,4]])

df = pd.DataFrame(data=data, index=index, columns=columns)
df['sumC'] = df.sum(axis=1)  # append the sums of the rows
df.loc['sumL']= df.sum()     # append the sums of the columns
df
A B sumC
red 4 10 14
green 1 4 5
sumL 5 14 19

Append the relative contributions of B and of green

We expand the matrix by a further column and a further row and use them to compute relative frequencies (see below).

def highlight_cells(x):
    df = x.copy()
    df.loc[:,:] = '' 
    df.iloc[1,1] = 'background-color: #53ff1a'
    df.iloc[1,3] = 'background-color: lightgreen'
    df.iloc[3,1] = 'background-color: lightblue'
    return df

df[r'B/sumC']         = df.values[:,1]/df.values[:,2]
df.loc[r'green/sumL'] = df.values[1,:]/df.values[2,:]

t = df.style.apply(highlight_cells, axis=None)
t

A B sumC B/sumC
red 4 10 14 0.714
green 1 4 5 0.8
sumL 5 14 19 0.737
green/sumL 0.2 0.286 0.263 1.09

Let's focus on the row with the green balls

From all green balls (= 5) is the portion of those with a letter B (=4) 0.8

$$ \frac{green\: balls\: with \:B}{all\: green\: balls} = \frac{4}{5} = 0.8 $$

Note that this value already corresponds to the conditional probality \(P(B \mid green)\)

$$ $$

Let's focus on the column with the balls with letter B

From all balls with letter B (= 14) is the portion of those that are green (=4) 0.286

$$ \frac{green\; balls\; with\; B}{all\; balls\; with\; letter\; B} = \frac{4}{14} = 0.286 $$

Note that also this value already corresponds to the conditional probality \(P(green \mid B)\)

$$ $$
$$ $$

Contingency table with the probabilities

We find the probabilities by dividing the frequencies by the sum of balls.

columns = np.array(['A', 'B'])
index   = np.array(['red', 'green'])
data    = np.array([[4,10],[1,4]])
data    = data/np.sum(data)

df = pd.DataFrame(data=data, index=index, columns=columns)
df['sumC'] = df.sum(axis=1)  # append the sums of the rows
df.loc['sumL']= df.sum()     # append the sums of the columns
df
A B sumC
red 0.211 0.526 0.737
green 0.053 0.211 0.263
sumL 0.263 0.737 1.000
$$ $$

Append the relative contributions of B and of green

df[r'B/sumC']         = df.values[:,1]/df.values[:,2]
df.loc[r'green/sumL'] = df.values[1,:]/df.values[2,:]
t = df.style.apply(highlight_cells, axis=None)
t

A B sumC B/sumC
red 0.211 0.526 0.737 0.714
green 0.0526 0.211 0.263 0.8
sumL 0.263 0.737 1 0.737
green/sumL 0.2 0.286 0.263 1.09

$$ $$

Note the formula in the cells

columns = np.array(['-----------A----------', '---------B----------', '----------sumC--------',  '--------B/sumC--------'])
index   = np.array(['red', 'green', 'sumL',  'green/sumL'])
data    = np.array([['...','...','...','...'],
                    ['...', '$P(B \cap green)$', '$P(green)$', '$P(B \mid green)$'],
                    ['...','$P(B)$','...','...'],
                    ['...','$P(green \mid B)$','...','...'] ])
df = pd.DataFrame(data=data, index=index, columns=columns)
t = df.style.apply(highlight_cells, axis=None)
t

-----------A---------- ---------B---------- ----------sumC-------- --------B/sumC--------
red ... ... ... ...
green ... \(P(B \cap green)\) \(P(green)\) \(P(B \mid green)\)
sumL ... \(P(B)\) ... ...
green/sumL ... \(P(green \mid B)\) ... ...

$$ $$

Conditional probability: Let's focus on the row with the green balls

The probability to get a ball with B out of all green balls is 0.8

$$ P(B \mid green) = \frac{P(green\: balls\: with \:B)}{P(all\: green\: balls)} = \frac{P(green \cap B)}{P(green)} = \frac{0.211}{0.263} = 0.8 $$
$$ $$

Conditional probability: Let's focus on the column with the balls with letter B

The probability to get a green ball out of all balls with a B is 0.286

$$ P(green \mid B) = \frac{P(green\; balls\; with\; B)}{P(all\; balls\; with\; letter\; B)} = \frac{P(green \cap B)}{P(B)} = \frac{0.211}{0.737} = 0.286 $$
$$ $$

Bayes rule

Given \(P(green \mid B\)) find \(P(B \mid green)\) :

$$ P(B \mid green) = \frac{P(green \mid B) \cdot P(B)}{P(green)} = \frac{0.286 \cdot 0.737}{0.263} = \frac{0.211}{0.263}= 0.8 $$
$$ $$

and given \(P(B \mid green)\) find \(P(green \mid B\)):

$$ P(green \mid B) = \frac{P(B \mid green) \cdot P(green)}{P(B)} = \frac{0.8 \cdot 0.263}{0.737} = \frac{0.211}{0.737} = 0.286 $$

Applying the Bayes rule means that we walk from the element most right in the matrix to the element at the bottom of the matrix and vice versa:

show_frequencies()

png

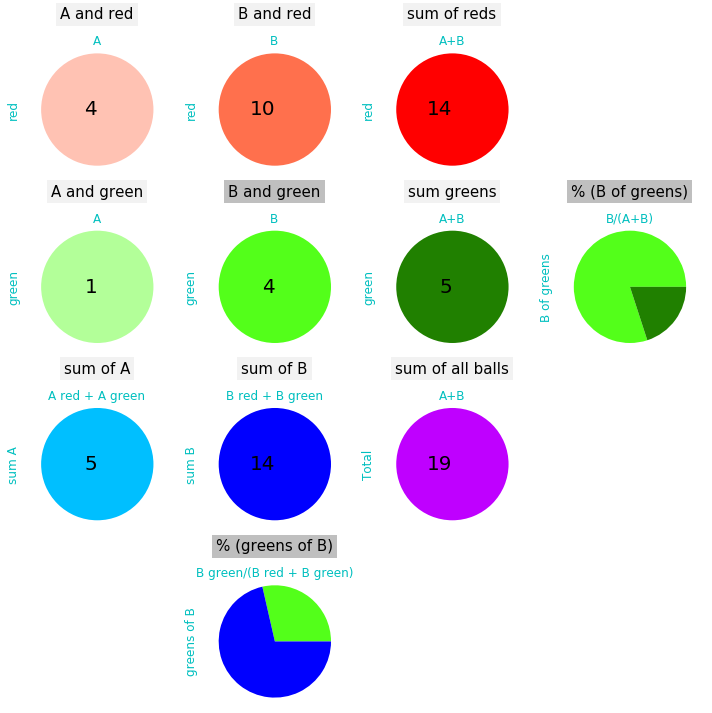
def show_frequencies():
    px = 4; py = 4


    figsize(10, 10)
    fontSize1 = 15
    fontSize2 = 12
    fontSize3 = 20

    A1 = 4;     A2 = 10;       A3 = A1+A2
    B1 = 1;     B2 =  4;       B3 = B1+B2
    C1 = A1+B1; C2 = A2+B2;   C3 = A3+B3

    data = np.array([[A1, A2, A3],
                     [B1, B2, B3],
                     [C1, C2, C3] ])

    clr     = np.array([ ['#ffc2b3', '#ff704d', '#ff0000'],
                         ['#b3ff99', '#53ff1a', '#208000'], 
                         ['#00bfff', '#0000ff', '#bf00ff']   ])


    title  = np.array([['A and red', 'B and red', 'sum of reds',
                       '$P(B|red) = \\frac {P(A\\cap red)}{P(red)}$'           ],
                       ['A and green', 'B and green', 'sum greens',   '% (B of greens)'     ],
                       ['sum of A', 'sum of B', 'sum of all balls',' '        ],
                       [' ', '% (greens of B)', '',  ' '     ],                  
                  ]  )

    xlabel = np.array([ ['A', 'B', 'A+B', 'B/(A+B)'],
                        ['A', 'B', 'A+B', 'B/(A+B)'],
                        ['A red + A green', 'B red + B green', 'A+B', 'B/(A+B)'],
                        ['A', 'B green/(B red + B green)', 'A+B', 'B/(A+B)']       ]  )

    ylabel = np.array([ ['red',   'red',   'red',  'B of reds'],
                        ['green', 'green', 'green','B of greens'],
                        ['sum A', 'sum B', 'Total', '' ],
                        ['green', 'greens of B', 'green', ' '],    ])



    f, ax = plt.subplots(px, py, sharex=True, sharey=True, edgecolor='none')  #, facecolor='lightgrey'

    for i in range(px-1):
        for j in range(py-1):

            patches, texts =ax[i,j].pie([data[i,j]], labels=[str(data[i,j])], #autopct='%1.1f%%',
                            shadow=False, startangle=90, labeldistance=0.0,
                            colors = [clr[i,j]])
            texts[0].set_fontsize(fontSize3)
            ax[i,j].set_title(title[i,j], position=(0.5,1.2), bbox=dict(facecolor='#f2f2f2', edgecolor='none'), fontsize= fontSize1)
            if i*j==1 :
                ax[i,j].set_title(title[i,j], position=(0.5,1.2), bbox=dict(facecolor='#bfbfbf', edgecolor='none'), fontsize=fontSize1)

            ax[i,j].set_xlabel(xlabel[i,j], fontsize=fontSize2, color='c')    
            ax[i,j].xaxis.set_label_position('top') 

            ax[i,j].set_ylabel(ylabel[i,j], fontsize=fontSize2, color='c')

            ax[i,j].axis('equal')

        j += 1
        if (i == 1):
            p = data[i,-2]/data[i,-1]; o = p/(1-p)
            patches, texts =ax[i,j].pie([o,1], #autopct='%1.1f%%',
                            shadow=False, startangle=0.0, labeldistance=0.0, 
                            colors = [clr[i,1], clr[i,2] ] )
            texts[0].set_fontsize(fontSize3)
            ax[i,j].set_title(title[i,j], position=(0.5,1.2), bbox=dict(facecolor='#bfbfbf', edgecolor='none'), fontsize=fontSize1)
            ax[i,j].set_xlabel(xlabel[i,j], color='c', fontsize=fontSize2)
            ax[i,j].xaxis.set_label_position('top') 
            ax[i,j].set_ylabel(ylabel[i,j], fontsize=fontSize2, color='c')
            ax[i,j].axis('equal')
        else: 
            ax[i,j].plot(0,0)
            ax[i,j].set_frame_on(False)

    i = px-1; 
    for j in range(py):
        if j==1:
            p = data[1,1]/data[2,1]; o = p/(1-p)
            patches, texts =ax[i,j].pie([o,1], #autopct='%1.1f%%',
                        shadow=False, startangle=0.0, labeldistance=0.0, 
                        colors = [clr[1,1], clr[2,1] ])
            texts[0].set_fontsize(fontSize3)
            ax[i,j].set_title(title[i,j], position=(0.5,1.2), bbox=dict(facecolor='#bfbfbf', edgecolor='none'), fontsize=fontSize1)

            ax[i,j].set_xlabel(xlabel[i,j], color='c', fontsize=fontSize2)
            ax[i,j].xaxis.set_label_position('top') 
            ax[i,j].set_ylabel(ylabel[i,j], fontsize=fontSize2, color='c')
            ax[i,j].axis('equal')
            ax[i,j].set_facecolor('y')
        else: 
            ax[i,j].plot(0,0)
            ax[i,j].set_frame_on(False)    

    plt.tight_layout()
    plt.show()

from IPython.display import HTML

# HTML('''<script> $('div .input').hide()''') #lässt die input-zellen verschwinden

HTML('''<script>
code_show=true; 
function code_toggle() {
 if (code_show){
 $('div.input').hide();
 } else {
 $('div.input').show();
 }
 code_show = !code_show
} 
$( document ).ready(code_toggle);
</script>
<form action="javascript:code_toggle()"><input type="submit" value="Click here to toggle on/off the raw code."></form>''')