The Fibonacci sequence in Mondrian style

Di 25 September 2018
GenerativeArt
Peter Schuhmacher
#Python

The sequence

The Fibonacci sequence is a famous formula in mathematics. Each number in the sequence is the sum of the two numbers that precede it. The mathematical equation is

$$ x_{n+2}= x_{n+1} + x_n $$

So, the sequence is: $0, 1, 1, 2, 3, 5, 8, 13, 21, 34, ...$ and so on.

There is a lot of fascination around the Fibonacci sequence including the ranking myths to be the secret code that governs the architecture of the universe - that's something !

The teaser

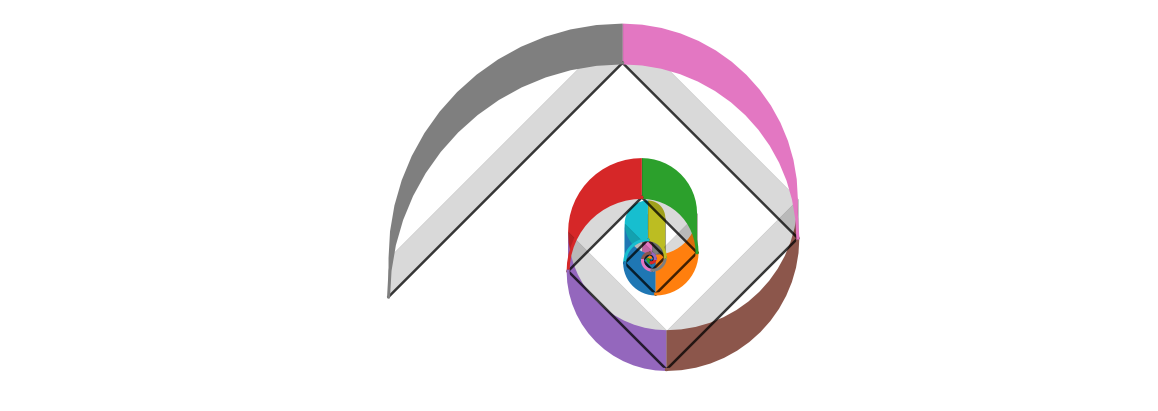
Computing the sequence is simple. But ploting the curve with the changing radius has a tricky detail: The centers of the circle segments change the position for each segment. So the question is how to program this sequence of movements without tons of lines with if-then-else-more if- more else-....

We have found a lean implementation when we realized that the movement of the center follows a simple pattern $0, 1, 0, -1, 0, 1, ....$, which has to be multiplied with $dR$ and summed up. We can generate that series with a trigonometric $sin()$-function.

The display

The graphical display is not fully 3-dimensional. Rather the curve is plotted twice with a displacement $dy$ which is filled with color between. So the image lives from the visual illusion. Since the Fibonacci series is growing fast we display the curve with the square root of the radius, $\sqrt{R}$ , rather then with the original $R$.

The style

Even when the resulting image has a circular basic pattern it has some similarities with the artistic style of Piet Mondrian in his avant-gardistic phase: flat colors, large portions of the area in white, the black secants as space dividers.

The code

import numpy as np
import matplotlib.pylab as plt
np.set_printoptions(linewidth=200, precision=3)

ns = 18                                # input: number of segments
mp = 15                                # input: resolution of the line segments

R = np.array([1,2])                    # generate the Fibonacci series which gives the radius
for i in range(2, ns):  
    R = np.append(R, R[-1] + R[-2])
R = R**0.6                             # empirical scaling for the graphics

dR = np.r_[0,np.diff(R)]               # build the differences bewteen the R_i
phi0 = np.linspace(0,1,mp)*0.5*np.pi   # compute the angels

xc, yc = 0.0, 0.0                      # initial center of the circle
t = np.arange(ns)                      # generate the movements of the circle center
cx = np.r_[0,np.sin(0.5*np.pi*t)]      # change of the center of the circle, x
cy = np.r_[0,np.sin(0.5*np.pi*(t-1))]  # change of the center of the circle, y

fig, ax = plt.subplots(figsize=(20,7));
for ir,r in enumerate(R):
    phi1= ir*0.5*np.pi;                                           # movement of the phase
    phi = (phi0 + phi1)                                           # angel
    xc  = xc + dR[ir]*cx[ir];      yc  = yc + dR[ir]*cy[ir]       # move the center of the circle
    x   = r*np.cos(phi) + xc;      y   = r*np.sin(phi) + yc       # compute the circle in cartesian coordinates
    gx  = np.array([x[0],x[-1]]);  gy = np.array([y[0],y[-1]])    # set the straight lines

    #---- graphics --------------------------
    plt.plot(gx,gy, c='k', lw=2.5,alpha=0.75)
    plt.fill_between(gx,gy,gy+25, color='k', lw=0.5,alpha=0.15)
    plt.plot(x,y, lw=3)
    plt.fill_between(x,y,y+25,label=str(ir))

plt.axis('equal');plt.axis('off');plt.show()
fig.savefig('fibonacci_mondrian.png', transparency=True)

png