Compass notation

We introduce a local compass notation for the variable $\mathbf{T}$ and it's coefficients $\mathbf{D}$. In compass notation we indicate the grid points with capitals and the faces to the neighbouring cells with small letters.

            N  
            |
            |
     nw-----n-----ne
      |     |     |
      |     |     |
W-----w-----P-----e-----E
      |     |     |
      |     |     |
     sw-----s-----se
            |  
            |
            S

$$ \begin{array}{c|c|c} \textrm{Compass notation}\\ \hline T_W = T_{i-1,j} & T_P = T_{i,j} & T_E = T_{i+1,j} \\ \hline D_W = D_{i-1,j} & D_P = D_{i,j} & D_E = D_{i+1,j} \\ \hline \end{array} $$

Finite Volume Method (FVM) 1-dimensional

The basic equation

The stationary diffusion equation may be written as

$$ \nabla\,(\Gamma\, \nabla T) + f = (\Gamma\,T_{x})_x+ f = 0 $$

and the time dependent (= instationary) as

$$ \begin{align} T_t & = \nabla\,(\Gamma\, \nabla T) + f \\ & = (\Gamma\,T_{x})_x+ f \\ \end{align} $$

$T$ descibes the status of a of quantity, the temperature e.g., $\Gamma$ is the diffusion coefficient, and $f$ stands for an additional, external source (as solar heating e.g.). The diffusion equation describes the change of the heat flux. If $\mathbf{H}$ is the heat flux, then diffusion is defined by the following generic set of equations:

$$ \begin{align} \mathbf{H} & = \Gamma \nabla T \\ \nabla\mathbf{H} & = \nabla(\Gamma \nabla T) \\ \end{align} $$

which drives the change of $T$.

Divergence theorem

The divergence theorem is the base for the finite volume method (FVM). So let's recapitulate some identities:

\begin{equation} \begin{array}{rclcl} \iiint \limits_{\Delta V} \nabla \mathbf{F} \, \mathrm{d}V & = & \iint \limits_{\Delta \Omega} \mathbf{F} \cdot \mathbf{n}\cdot \mathrm{d}S & & \textrm{Divergence-Theorem} \\ \overline{\nabla \mathbf{F}}\cdot \Delta V & = & \iint \limits_{\Delta \Omega} \mathbf{F} \cdot \mathbf{n}\cdot \mathrm{d}S \\ \overline{\nabla \mathbf{F}} & = & \frac{1}{\Delta V} \iint \limits_{\Delta \Omega} \mathbf{F} \cdot \mathbf{n}\cdot \mathrm{d}S \end{array} \end{equation}

Let's have a look at the right hand side: The surface of a control volume (CV) is defined by the straight-line segements of each side. In the 1 dimensional case the CV has 2 sides, $S_e$and $S_w$. The positive flux of the divergence theorem is defined as the normal outward flux, $\mathbf{H}_e + \mathbf{H}_w$. But since we define the direction of the $\mathbf{\hat{x}}$ -axis as positive direction the normal outward flux will have the form, $\mathbf{H}_e - \mathbf{H}_w$.

FVM Ansatz

The principle of the finite volume method FVM is:

integrate the equation over the control volume CV
Use the divergence theorem to replace the divergence terms by the flux through the surface integrated over the surface
replace the flux by the expression with the temperature gradient

$$ \begin{equation} \begin{array}{rclcl} \nabla(\Gamma\nabla T) + f &=& 0 \\ \mathbf{F} & := & \Gamma \nabla T \\ \nabla \mathbf{F} + f &=& 0 \\ \iiint \limits_{\Delta V} \nabla \mathbf{F} \, \mathrm{d}V + \iiint \limits_{\Delta V} f \, \mathrm{d}V & = & \iint \limits_{\Delta \Omega} \mathbf{F} \cdot \mathbf{n}\cdot \mathrm{d}S + \iiint \limits_{\Delta V} f \, \mathrm{d}V \\ \overline{\nabla \mathbf{F}}_P \cdot \Delta V_P + \overline{f_P} \cdot \Delta V_P & = & \iint \limits_{\Delta \Omega} \mathbf{F} \cdot \mathbf{n}\cdot \mathrm{d}S + \overline{f_P} \cdot \Delta V_P\\ \end{array} \end{equation} $$

With $\mathbf{F} = \Gamma \nabla \phi$ this gives for the right hand side of the divergence theorem:

$$ \begin{equation} \begin{array}{rclcl} \iint_{S} \mathbf{F} \cdot d\mathbf{S} & = & \sum_{f=faces} (\mathbf{F} \cdot \mathbf{S})_f \\ & = & \mathbf{F}_e \, \mathbf{S}_e - \mathbf{F}_w \, \mathbf{S}_w \\ & = & (\Gamma \nabla T)_e \, \mathbf{S}_e - (\Gamma \nabla T)_w \, \mathbf{S}_w \\ & = & \Gamma_e \frac{\partial T}{\partial x}|_e \, S_e - \Gamma_w \frac{\partial T}{\partial x}|_w \, S_w \\ & = & \Gamma_e \frac{T_E - T_P}{d_E} \, S_e - \Gamma_w \frac{T_P - T_W}{d_W} \, S_w \end{array} \end{equation} $$

and using the compass notation we get the following stencil for the system matrix

$$ \begin{array}{c|c|c|c} \hline T_W & T_P & T_E & b_P\\ \hline D_W = \frac{\Gamma_w S_w}{d_W} & D_P = -D_W - D_E & D_E = \frac{\Gamma_e S_e}{d_E} & \overline{f_P}\cdot \Delta V_P\\ \hline \end{array} $$

Fixed boundary condition

For a fixed boundary value on face $w$ at the left/west side of the domain we can write:

$$ \begin{equation} \begin{array}{rclcl} \overline{\nabla \mathbf{F}}_P \cdot \Delta V_P + \overline{f_P} \cdot \Delta V_P & = & \iint \limits_{\Delta \Omega} \mathbf{F} \cdot \mathbf{n}\cdot \mathrm{d}S + \overline{f_P} \cdot \Delta V_P\\ & = & \Gamma_e \frac{T_E - T_P}{d_E} \, S_e - \Gamma_{\tilde{w}} \frac{T_P - T_{\tilde{w}}}{d_{\tilde{w}}} \, S_{\tilde{w}} + \overline{f_P} \cdot \Delta V_P\\ \end{array} \end{equation} $$

We approximate the $\tilde{w}$-labeld terms with

$$ \begin{array}{c c c c} \Gamma_{\tilde{w}}=\Gamma_w, & S_{\tilde{w}}=S_w, & d_{\tilde{w}}=d_w = x_P - x_w & D_w, = \frac{\Gamma_w S_w}{d_w}\\ \end{array} $$

So we get the following stencil for the system matrix at the west boundary

$$ \begin{array}{c|c|c|c} \hline & T_P & T_E & b_P\\ \hline D_W = 0 & D_P = 0 - D_E & D_E = \frac{\Gamma_e S_e}{d_E} & Tfix_w \cdot D_w + \overline{f_P}\cdot \Delta V_P\\ \hline \end{array} $$

Flux/gradient boundary condition

For a Neumann boundary condition on face e the flux has to be prescribed. Since the term $\Gamma_e \frac{T_E - T_P}{d_E} \, S_e $ is the flux at $e$ it can be replaced by a perscribed value. So we get the following stencil for the system matrix at the east boundary:

$$ \begin{array}{c|c|c|c} \hline T_W & T_P & T_E & b_P\\ \hline D_W = \frac{\Gamma_w S_w}{d_W} & D_P = -D_W - 0 & D_E = 0 & Tflux_e + \overline{f_P}\cdot \Delta V_P\\ \hline \end{array} $$

Implicit (Euler backward) time schema

In the implicit time schema the tendency term $\mathbf{T}_t$ is discretizised as

$$ \mathbf{T}_t = \frac{ \mathbf{T}^{n} - \mathbf{T}^{n-1} }{\Delta t} = \mathbf{D \, T}^n + \mathbf{f} $$

The unknown quantity $\mathbf{T}^{n}$ is on the left side of the equation including the equation system which has to be solved at each time step

$$ \begin{align} \mathbf{T}^{n} - \Delta t \, \mathbf{D \, T}^n & = \mathbf{T}^{n-1} + \Delta t \,\mathbf{f} \\ (\mathbf{I} - \Delta t \, \mathbf{D}) \, \mathbf{T}^n & = \mathbf{T}^{n-1} + \Delta t \,\mathbf{f} \end{align} $$

The stencil for the implicit schema is now

$$ \begin{array}{c|c|c|c} \hline T_W & T_P & T_E & b_P\\ \hline D_W = -\Delta t \frac{\Gamma_w S_w}{d_W} & D_P = 1-(-D_W - D_E) & D_E = -\Delta t \frac{\Gamma_e S_e}{d_E} & \overline{f_P}\cdot \Delta V_P\\ \hline \end{array} $$

Introducing $\tilde{\mathbf{A}}$ we find the following form of discretisation:

$$ \begin{align} \tilde{\mathbf{A}} & := (\mathbf{I} - \Delta t \,\,\mathbf{D} ) \\ \tilde{\mathbf{A}} \mathbf{u}^n & = \mathbf{b}^{n-1} \end{align} $$

Implementation

import numpy as np
import pandas as pd
import scipy.sparse as sps
from scipy.sparse.linalg import bicgstab
import matplotlib.pylab as plt

np.set_printoptions(linewidth=200, precision=3)

Signals

This are auxiliary functions to initialize the parameter values. We have prepared a collection of signals here: https://alpynepyano.github.io/healthyNumerics/posts/ecg-waves-python.html

class signal:
    def scale(self,t):            return (t-t.min())/(t.max()-t.min())
    def add_noise(self,t):        return np.random.randn(t.shape[0])
    def line(self,t):             return self.scale(t)
    def uSignal(self,t):          return np.array(0.5*np.sign(t) + 0.5,dtype=int)
    def wSignal(self,t,dt):       return self.uSignal(t)-self.uSignal(t-dt)
    def expSignal(self,t):        return np.exp(t)
    def minus_exp_square(self,t): return np.exp(-t**2)

The FVM grid

We generate a 1-dimensional grid with irregular spacing between the grid points. We start with the location of the faces and compute then the grid point in the center.

class grid1D:
    def __init__(self, nxc, Lx, sCase):
        self.nxc = nxc                                                         # number of faces
        self.Lx = Lx                                                           # length of x-domain
        sT = {'stretch_regular':self.stretch_regular,                          # mapping of stretching types
              'stretch_exp'    :self.stretch_exp}
        self.stretchT = sT[sCase]                                              # selects the type of stretching
    def scale(self, a):                    return (a-a.min())/(a.max()-a.min())# scaling to [0..1]
    def xi(self):                          return  np.linspace(0,1.0,self.nxc) # logical/computational grid
    def stretch_regular(self):             return  np.linspace(0,1.0,self.nxc) # regular grid, no stretching
    def stretch_exp(self):                                                     # exponantial stretching
        ix = self.xi();                    return  self.scale(np.exp(2*ix))
    def xc(self):                          return self.Lx*self.stretchT()      # face x-coordinate
    def xp(self):                          return self.centerPoint(self.xc())  # center point coordinate
    def dx(self):                                                              # spacing between P's
        xc = self.Lx*self.stretchT()
        x  = np.r_[xc[0],self.centerPoint(xc),xc[self.nxc-1]]
        return np.diff(x)
    def centerPoint(self,x): mx=x.shape[0]; return 0.5*(x[0:mx-1] + x[1:mx])    # center point P method
    def Swe(self):                          return np.ones((self.nxc))          # areas of the faces west-east
    def cvP(self):
        Swe = self.Swe(); mx=Swe.shape[0];
        return 0.5*(Swe[0:mx-1] + Swe[1:mx])*np.diff(self.xc())                 # volumes of the CV

#--- MAIN -------------------------------------------------------
#--- Input ------------------------------------------------------    
nxc = 28                               # number of faces/corners
Lx  = 0.02                             # length of x-domain
#Lx  = 0.3                             # length of x-domain
nxp = nxc-1                            # number of central points P     
#g  = grid1D(nxc,Lx,'stretch_regular') # 2 types
g   = grid1D(nxc,Lx,'stretch_exp')     # type of grid strechting

Graphics of the grid

#--- Graphics -----------------
#--- plot the grid ------------
xc = g.xc()                            # get the corners/faces points w, e
xp = g.xp()                            # get the central points P

def plot_grid(ax0,xc,xp, y_base=0):
    ax0.plot(xc, y_base+0*xc, c='k', ls='--', marker="|",ms=20, lw=2, alpha=0.5 )
    ax0.scatter(xp, y_base+0*xp,c='r', marker='o', s=90, alpha=0.75)
with plt.style.context('fast'):
    fig, ax0 = plt.subplots(figsize=(20,4))
    plot_grid(ax0,xc,xp)
    grid_legend = np.array(['xc: face points w', 'xp: center grid points P' ])
    plt.margins(0.1); plt.grid(axis='y'); plt.legend(grid_legend,prop={'size': 15})
    plt.title("Finite Volume Grid",fontsize=25, fontweight='bold')
    plt.show()

png

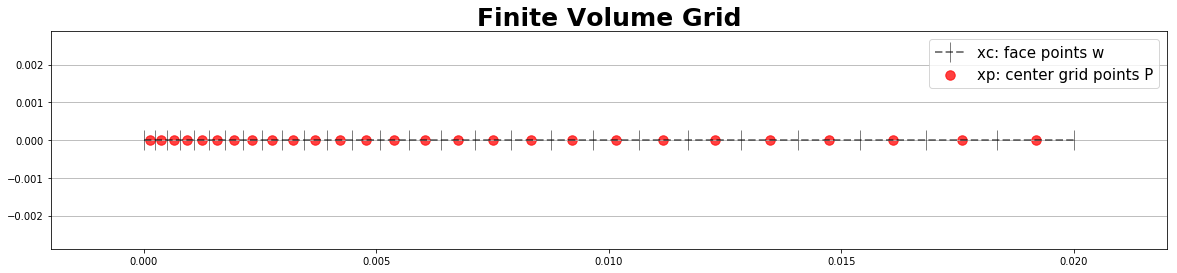
Parameters and boundary conditions

We will run the following case; which is given here: http://ftp.demec.ufpr.br/disciplinas/TM702/Versteeg_Malalasekera_2ed.pdf :

Case B

a plate with thikness: $L = 2 cm$
thermal conductivitiy, constant over the domain: $\Gamma = 0.5 \; W/(m \cdot K)$
uniform heat generation $q = 1000\; kW/m^3$
temperatur at the west boundary, constant: $T_w = 100^o C$
temperatur at the east boundary, constant: $T_e = 200^o C$

class system1D:
    def __init__(self,g,sig,case):
        self.g = g
        self.nxc = g.nxc
        self.nxp = self.nxc-1
        self.sig = sig
        self.case = case
    def b(self):        return np.zeros((self.nxp))             # initialize local rhs
    def DWE(self,g):    return self.gam()*g.Swe()/g.dx()        # build the non-zero elements of the system matrix  
    #----- input section ------------------------------------------------------------------------------
    def T(self):         
        if self.case=='B':   return 0.1*np.random.randn((self.nxp))  # initial value, random gauss [-0.1 .. +0.1]
        if self.case=='C':   return 273.0*np.ones((self.nxp))           
    def q(self,g):
        if self.case=='B':   return 1000*(10**3) *g.cvP()       # set source term
        if self.case=='C':   return 0.00                        # set source term
    def gam(self):
        if self.case =='B':  return 0.5*np.ones((self.nxc))     # set diffusion coefficient
        if self.case =='C':  return 0.1*np.ones((self.nxc))     # set diffusion coefficient
    def T_west_fix(self):
         if self.case =='B': return 100.0                       # set T_fix at w-boundary
         if self.case =='C': return 273.0                       # set T_fix at w-boundary
    def T_east_fix(self):
         if self.case =='B': return 200.0                       # set T_fix at e-boundary
         if self.case =='C': return 273.0                       # set T_fix at e-boundary

def insert_boundary_conditions(sT,DWE,b):
    #----- input section ------------------------------------------------------------------------------
    west_fix = True  #---- west boundary                       # select type of boundary condition at w
    if west_fix:
        b[0] = sT.T_west_fix() * DWE[0];  
    else: T_west_flux = 0; DWE[0] = T_west_flux

    east_fix = True   #---- east boundary                      # select type of boundary condition at e
    if east_fix:
        b[-1] =  sT.T_east_fix() * DWE[-1];
    else: DWE[-1] = 0.0
    return DWE,b

The analytical solution

def Tcase_B(x):  
    L, gamma, Q = 0.02, 0.5, 1000*10**3;
    Tw, Te = 100.0, 200.0;
    return  Tw + x*( (Te-Tw)/L +  0.5*Q*(L-x)/gamma)
x = xp.copy()
TB = Tcase_B(x)
with plt.style.context('fast'):
    fig, ax0 = plt.subplots(figsize=(20,4))
    plt.plot(x,TB,'o-');
    plt.title('Case B: analytical solution', fontweight='bold');
    plt.grid(axis='y');plt.show()

png

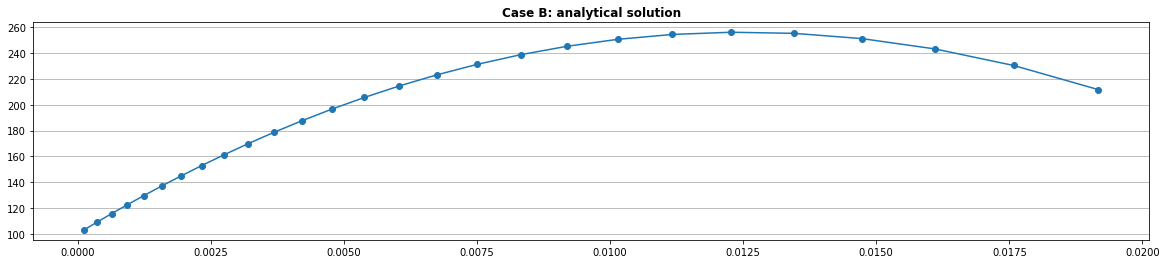
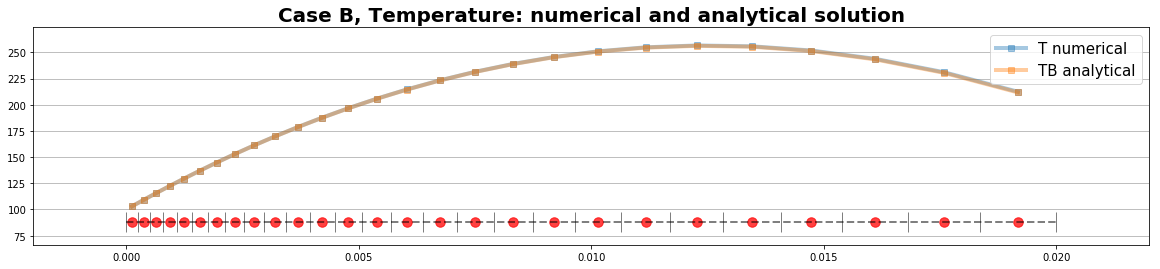
The numerical solution

The numerical solution hardly differs from the analytical solution. Both are computed on the stretched grid.

def solve_stationary_system(DWE,RHS,T):
    def print_convergence(cc):
        if cc==0 : print("bicg-stab: successful exit --> c =",cc)
        if cc >0 : print("bicg-stab: convergence to tolerance not achieved, number of iterations is = ", cc)
        if cc <0 : print("bicg-stab: illegal input or breakdown --> c =",cc)

    #---- center P ----
    DP = -DWE[0:nxp] - DWE[1:nxc];  
    #---- system matrix D ----
    DW =  DWE[1:nxp];   DE = DWE[1:nxp]
    D = sps.diags( diagonals=[DW, DP, DE],
                     offsets=[-1,  0,  1],
                     shape=(nxp, nxp), format='csr')
    #---- numerical solver
    X = bicgstab(D,-RHS,x0=T,tol=1e-06, maxiter=None);  
    print_convergence(X[1])
    return X[0]  # X[0] := solved T

#----- main --------------------
sig    = signal()                               # get access to the signals
sT     = system1D(g,sig,case='B')               # instantiate a system for this case
qT     = sT.q(g)                                # set the source term
#---- main ---------------------
DWE    = sT.DWE(g)                              # build the non-zero elements of the system matrix
bT     = sT.b()                                 # initialize the local rhs of this system
DWE,bT = insert_boundary_conditions(sT,DWE,bT)  # insert the boundary conditions: changes DWE and b
RHS    = bT+qT                                  # update the right hand side of the complete system
T      = sT.T()                                 # initialize T
T      = solve_stationary_system(DWE,RHS,T)     # run the numerical sover

bicg-stab: successful exit --> c = 0

Graphics

G = pd.DataFrame({ 'T numerical':T,
                  'TB analytical':TB
                 })
#print('T-TB', T-TB)
ybase = np.min(T)-0.1*(np.max(T)-np.min(T))

with plt.style.context('fast'):
    fig, ax0 = plt.subplots(figsize=(20,4))
    plt.plot(xp,G, marker='s',lw=4, alpha=0.4);
    plot_grid(ax0,xc,xp, y_base=ybase)
    grid_legend = np.array(['xc: face points w', 'xp: center grid points P' ])
    plt.legend(G.columns, prop={'size': 15})
    plt.margins(0.1); plt.grid(axis='y'); #plt.legend(prop={'size': 15})
    plt.title("Case B, Temperature: numerical and analytical solution",fontsize=20, fontweight='bold')
    plt.show()

png

A time dependent solution is given here

HealthyNumerics

An inplicite time dependent finite volume model (FVM) on an irregular grid for heat flow