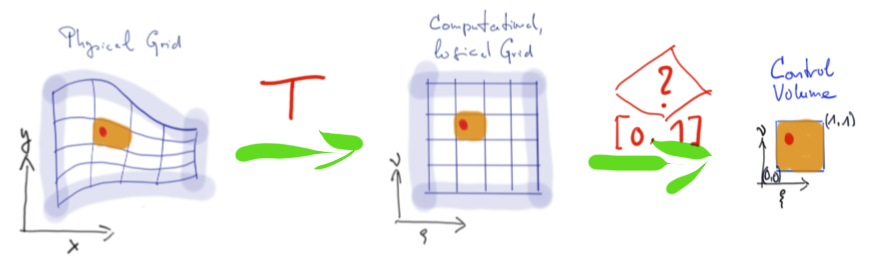
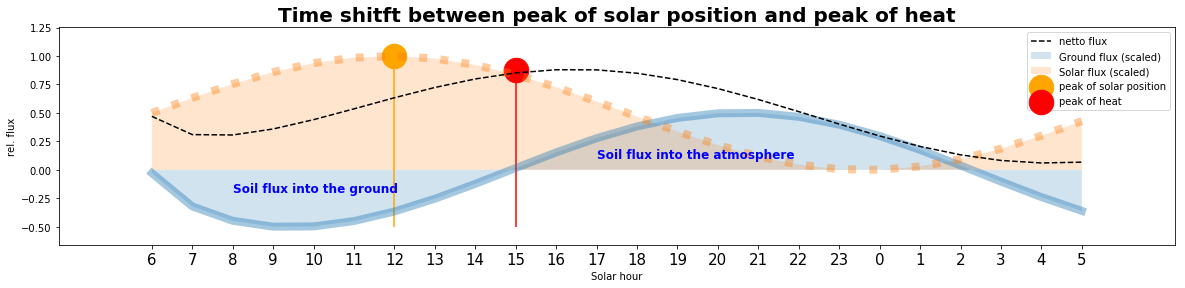
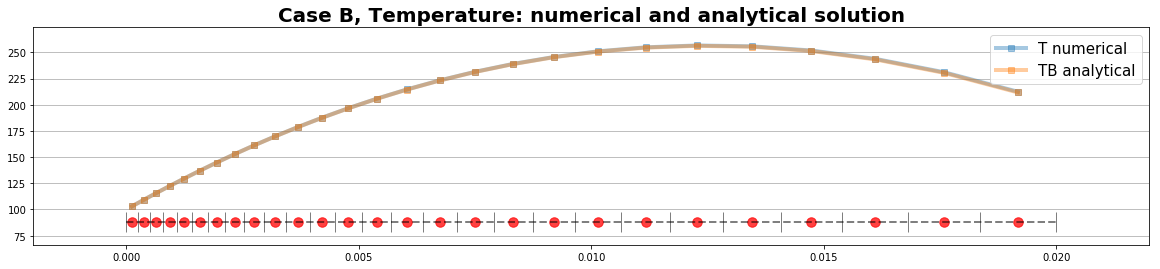
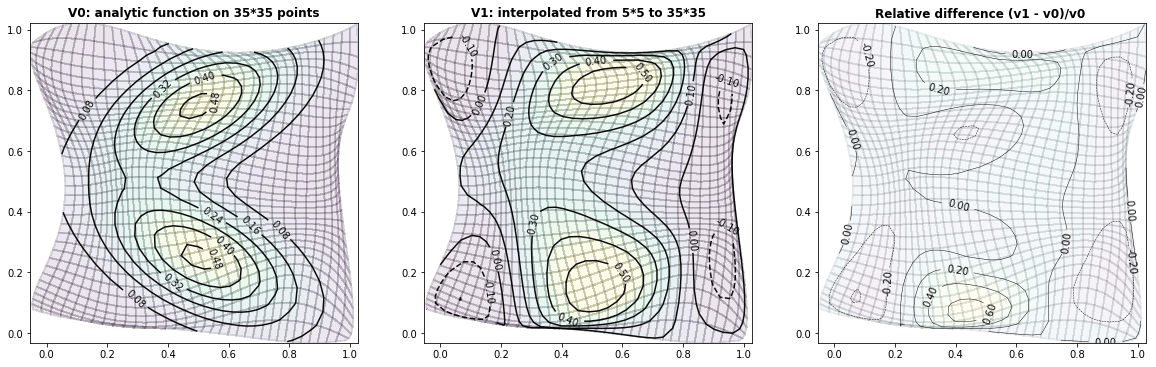
- Mi 06 Februar 2019
- ComputationalFluidDynamics
- Peter Schuhmacher
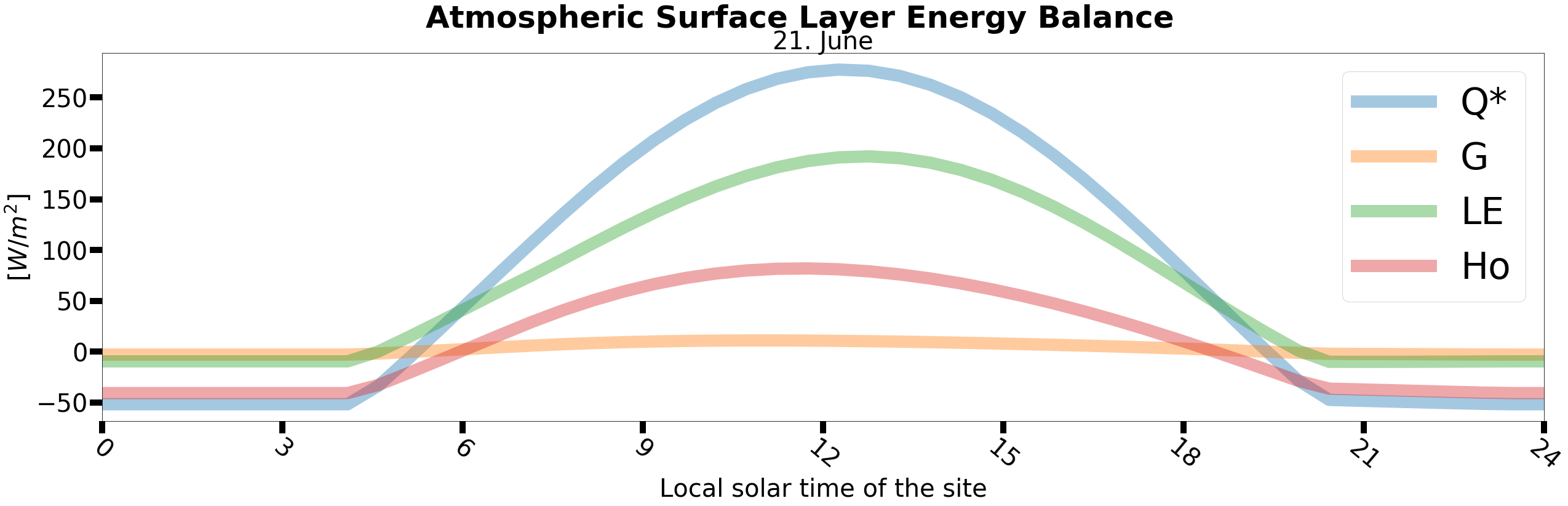
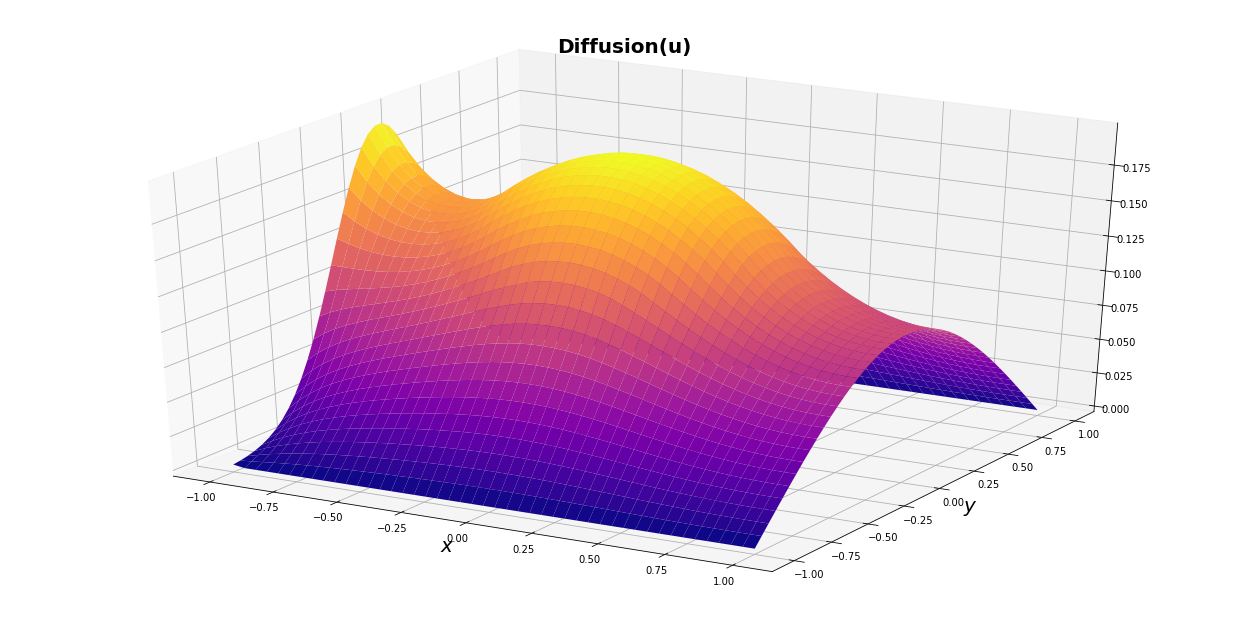
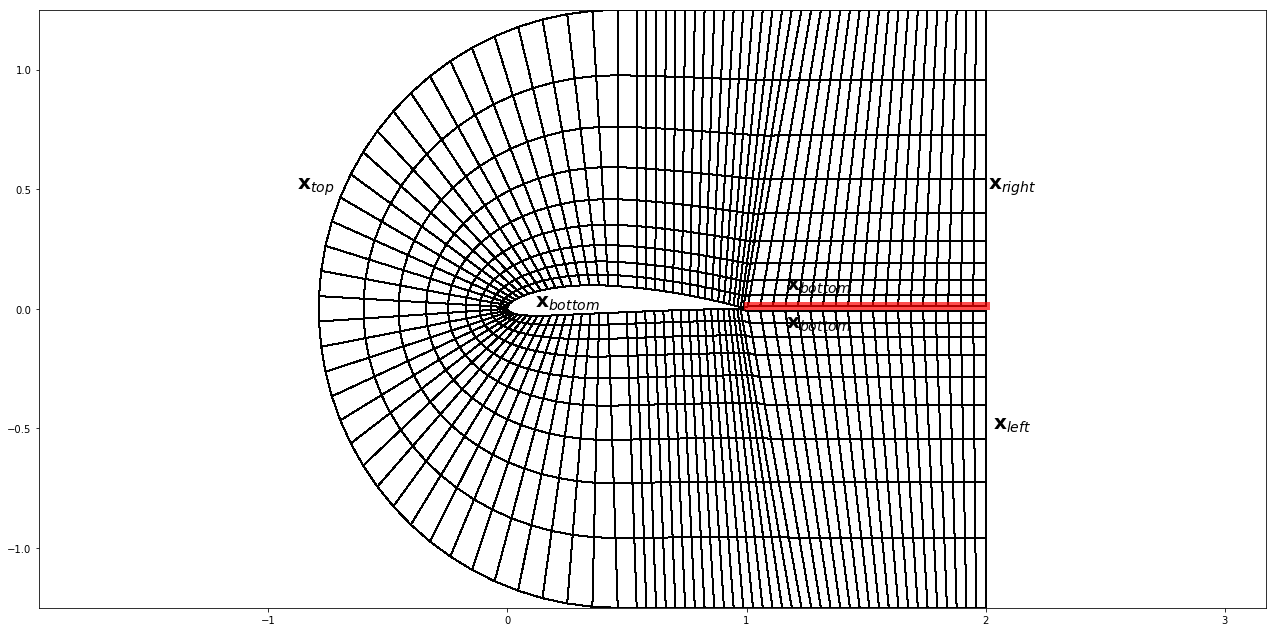
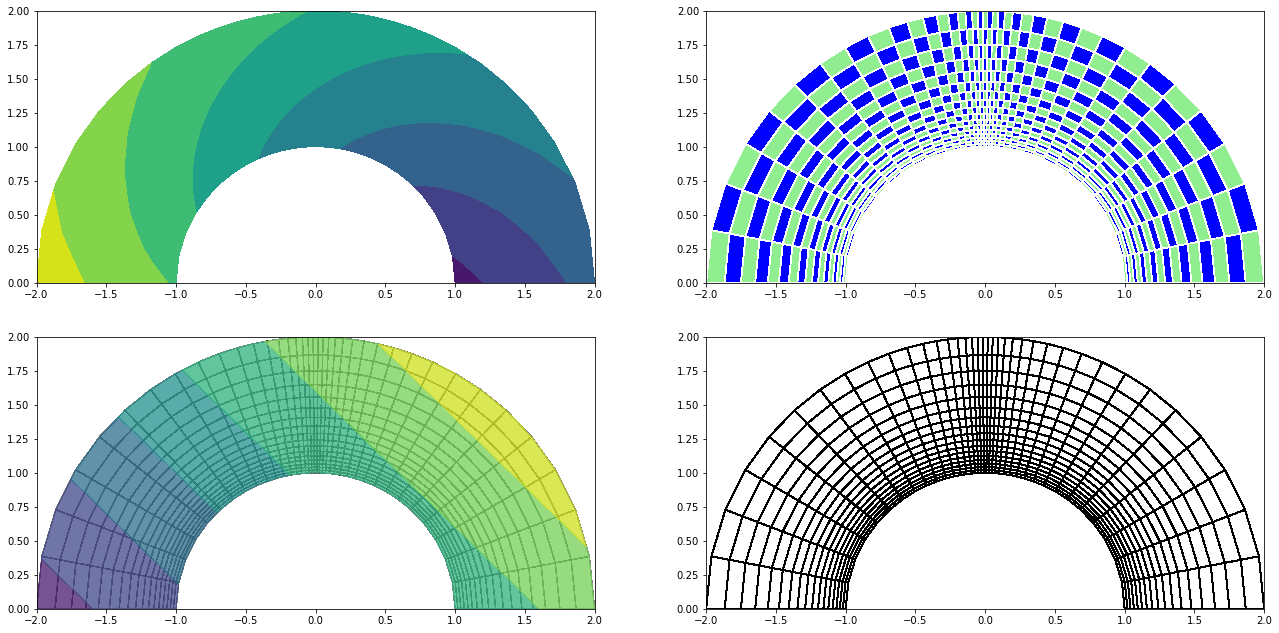
Moving Average = Diffusion = Markov Chain = Monte Carlo
We compare 4 numerical principles that have smoothing and/or time marching properties and show the similarities between them.