- Di 03 März 2020
- MachineLearning
- Peter Schuhmacher
MachineLearning: A simple but complete artificial Neural Network
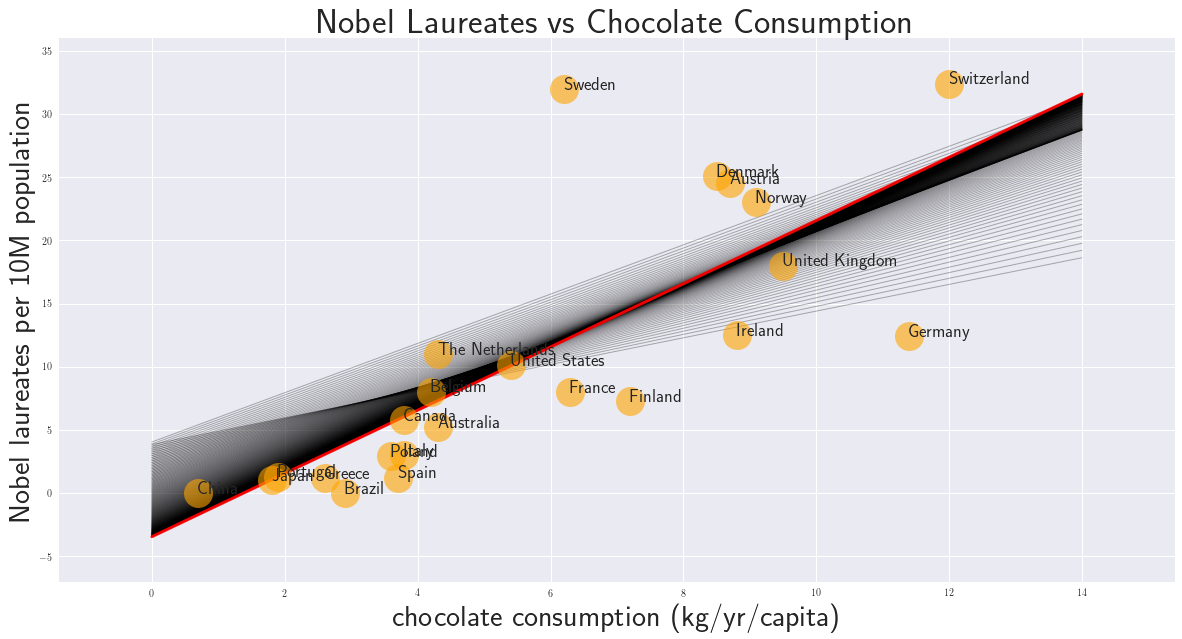
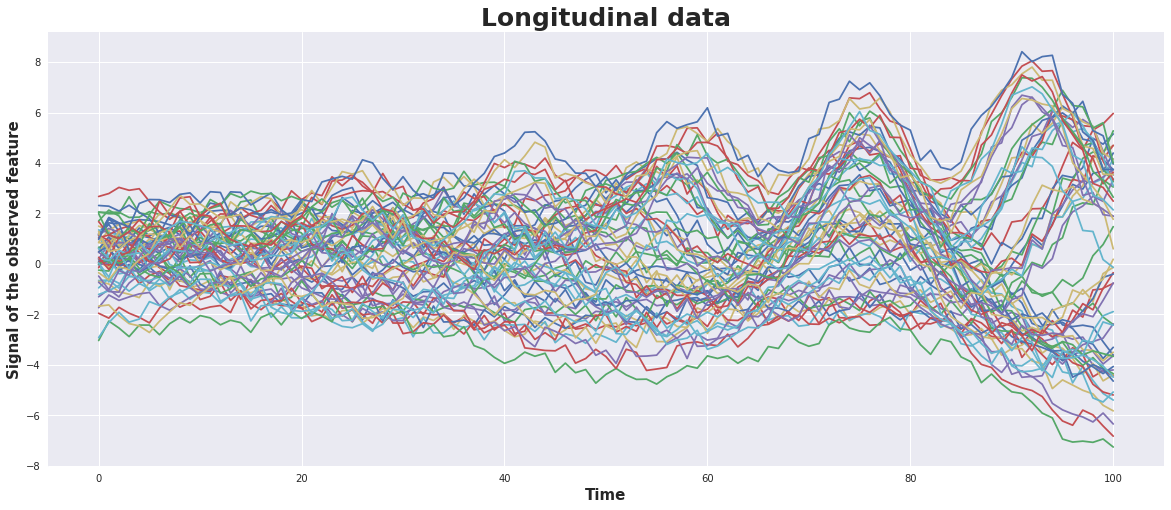
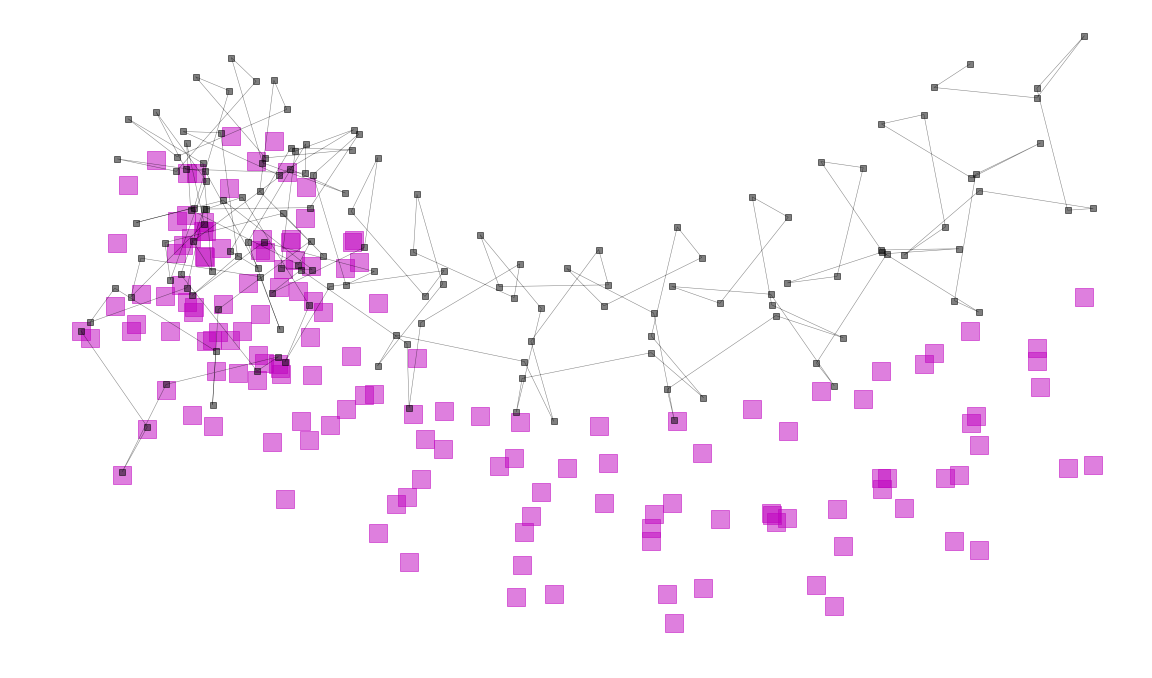
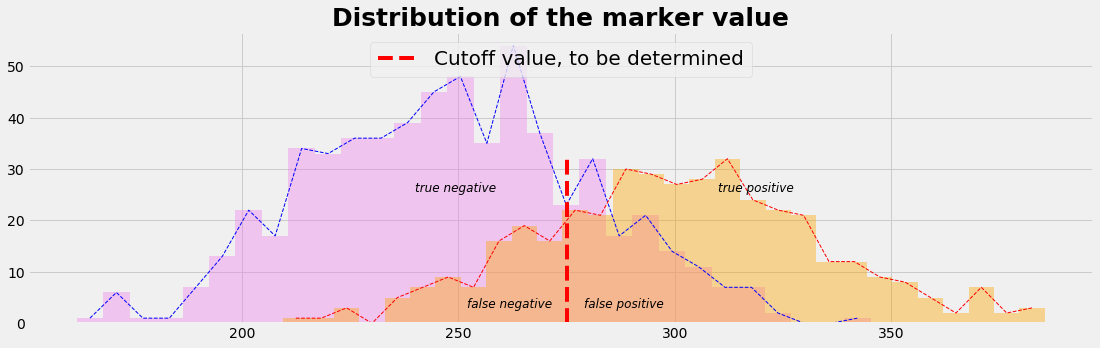
Artificial Neural Networks "learn" to perform tasks by considering examples. They do this without any prior knowledge. Instead, they automatically generate identifying characteristics from the examples that they process. Beside the success of an AI model the confusion or error matrix is an important tool. It gives a risk profile we have to deal with when using AI models.